ABSTRACT
멀티모달 대형 언어 모델(MLLMs)은 이미지와 텍스트를 동시에 다루며 다양한 일을 잘 수행하지만, 여전히 복잡한 수학적 추론에는 약점을 보입니다. 기존 연구들은 주로 데이터셋을 새로 만들거나 학습 방법을 조금씩 개선하는 데 집중했지만, 체계적인 수학 지식 설계나 모델 중심의 데이터 공간 설계는 상대적으로 소홀히 다뤄졌습니다. WE-MATH 2.0은 이러한 한계를 보완하기 위해 등장한 통합 시스템으로, 수학 지식 체계, 난이도별 데이터셋, 강화학습 기반 학습 방법, 그리고 종합 평가 도구를 결합하여 모델의 수학적 추론 능력을 향상시키는 것을 목표로 합니다.
이 시스템의 핵심은 네 가지입니다.
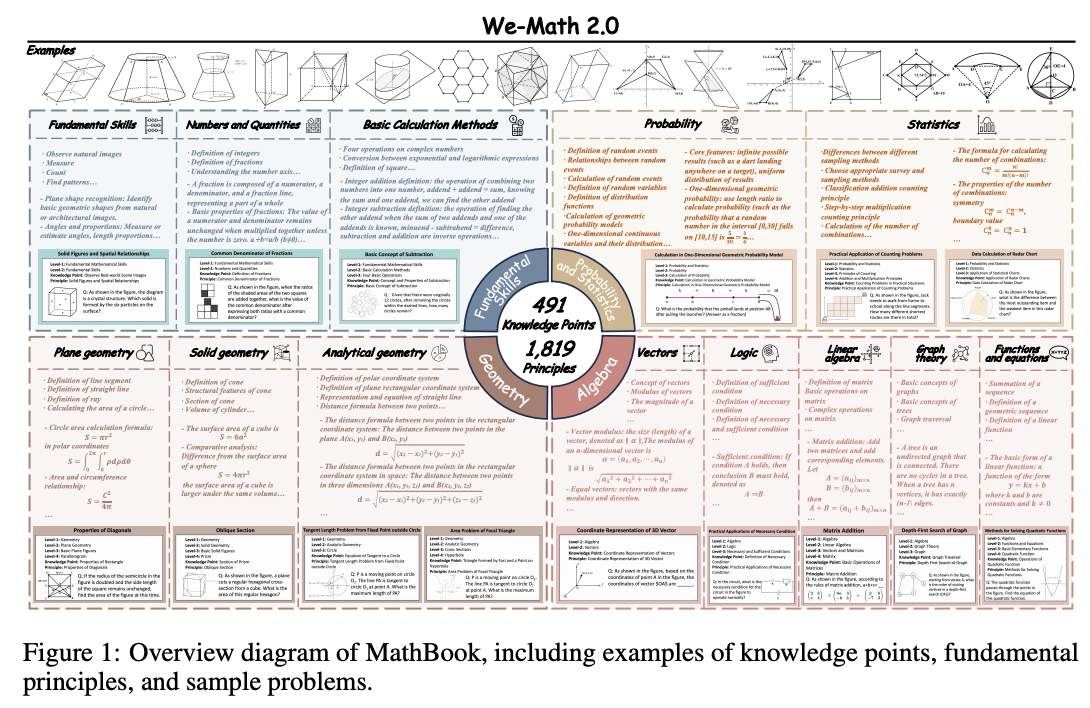
첫째, 수학 개념을 5단계로 나누어 491개의 지식 포인트와 1,819개의 원리를 담은 MathBook 지식 체계를 구축했습니다.
둘째, 데이터셋을 두 가지로 나눴는데, MathBook-Standard는 폭넓은 개념을 다루며 확장성이 높고, MathBook-Pro는 문제를 난이도 3차원 공간 속에서 변형하여 같은 문제를 7단계 버전으로 만들어 점진적인 학습이 가능하도록 했습니다.
셋째, MathBook-RL이라는 강화학습 학습법을 제안했는데, 이는 (1) 모델이 수학적 풀이 과정을 익히도록 하는 초기 파인튜닝과 (2) 쉬운 문제에서 어려운 문제로 점차 발전해가는 점진적 강화학습으로 이루어집니다.
넷째, MathBookEval이라는 평가 도구를 만들어 491개의 지식 포인트 전반을 아우르며, 정답뿐만 아니라 풀이 과정의 복잡성까지 확인할 수 있게 했습니다.
실험 결과, WE-MATH 2.0은 기존 널리 쓰이는 수학 벤치마크에서 경쟁력 있는 성과를 보였으며, 특히 MathBookEval에서는 높은 일반화 성능을 보여 실제적인 수학적 추론 능력을 강화했음을 입증했습니다. 즉, WE-MATH 2.0은 지식 체계화·난이도 설계·강화학습·평가까지 포함한 종합적인 학습 패키지로, MLLMs의 수학적 사고력을 근본적으로 끌어올리려는 시도라고 할 수 있습니다.
1 Introduction
멀티모달 대형 언어 모델(MLLMs)은 글과 그림을 함께 이해하고 다루면서 이미지 기반 질문답변(VQA), 글자 인식(OCR), 객체 탐지 같은 다양한 작업에서 좋은 성과를 보이고 있습니다. 하지만 여전히 복잡한 수학 문제를 풀고 추론하는 데에는 약점이 많습니다. 특히 문제를 새로운 방식으로 변형하거나 일반화하는 능력이 부족합니다.
지금까지 연구들은 크게 세 가지 방향으로 진행되었습니다.
- 새로운 수학 데이터셋 만들기
- Chain-of-Thought 같은 방식으로 단계별 추론을 유도하는 학습
- 커리큘럼(단계별 난이도 조절)을 활용한 강화학습(RL)
이 덕분에 성과가 있었지만 여전히 중요한 한계가 남아 있습니다.
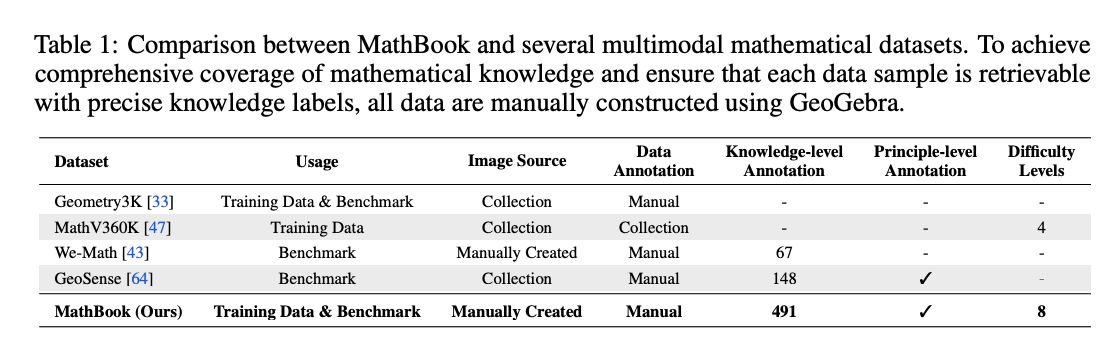
- (문제 1) 지식 체계 부족: 수학 분야 전반을 고르게 다루지 못하고, 데이터셋이 특정 영역에 치우쳐 있다.
- (문제 2) 모델 중심 난이도 설계 부족: 기존 난이도는 사람의 학습 단계를 기준으로 설계됐는데, MLLM의 학습 패턴과는 맞지 않는다.
- (문제 3) 일반화 부족: 어려운 문제는 풀지만, 그 문제를 구성하는 작은 하위 문제나 비슷한 유형 문제에는 약하다. 즉, 문제 풀이를 ‘암기’하는 것에 치중돼 있고, 진짜 추론 능력이 잘 안 늘어난다.
이 문제를 해결하기 위해 WE-MATH 2.0이라는 새로운 프레임워크를 제안합니다. 이 프레임워크는 크게 네 가지로 이루어집니다.
- MathBook Knowledge System
위키피디아와 교과서에서 지식을 뽑아내고, 계층적으로 정리해 전문가가 다듬어 만든 5단계 구조. 여기에는 491개의 지식 포인트와 1,819개의 원리가 포함됩니다. 즉, 수학 지식을 체계적으로 정리한 “수학 백과사전” 같은 것입니다. - MathBook-Standard & MathBook-Pro (데이터셋)
- MathBook-Standard는 균형 있게 다양한 문제를 담고, “한 문제에 여러 그림”, “한 그림에 여러 문제” 같은 확장 방식을 적용해 개념을 유연하게 학습할 수 있도록 만들었습니다.
- MathBook-Pro는 난이도를 세 가지 축(풀이 단계 복잡성, 시각적 복잡성, 문맥 복잡성)으로 정의해, 같은 문제를 7단계 난이도로 변형했습니다. 이렇게 해서 모델이 점진적으로 어려운 문제에 도전할 수 있습니다.
- MathBook-RL (강화학습 프레임워크)
두 단계로 구성됩니다.- Cold-Start Fine-tuning: 모델이 수학 풀이 과정을 “체계적 사고 방식(CoT)”으로 익히게 하는 초기 지도학습 단계.
- Progressive Alignment RL: 난이도를 점진적으로 높이며 학습하는 단계. 여기서 오류가 생기면 지식 단계 보완(쉬운 단계 문제로 돌아가 보완) 또는 모달리티 단계 보완(단일 시각 정보 문제로 단순화) 전략을 적용해 점진적으로 강화합니다.
- MathBookEval (평가 도구)
모든 491개 지식 포인트를 커버하는 평가 세트. 단순 정답률뿐 아니라 풀이 과정의 난이도와 다양성까지 평가 가능합니다.
실험 결과, WE-MATH 2.0은 기존 벤치마크에서도 경쟁력 있는 성과를 내고, 특히 새로운 평가 세트에서는 일반화와 추론 능력이 크게 향상되었음을 보여주었습니다.
2 Related Work
최근 연구에서 시각적 수학 추론(Visual Mathematical Reasoning), 즉 "그림·도형이 포함된 수학 문제를 모델이 이해하고 푸는 능력"을 키우려는 시도가 활발하게 이루어지고 있습니다.
연구 흐름은 크게 세 가지입니다.
- 평가 벤치마크 개발
- MathVista, MathVision: 모델의 전반적인 성능을 평가하는 종합 벤치마크.
- MathVerse: 텍스트 정보가 풍부할수록 모델이 더 잘 푼다는 점을 발견.
- Dynamath: 문제를 살짝 바꾼 "유사 문제"에서도 성능을 유지하는지(견고성·robustness)를 평가.
- 방법론 개선
- Math-LLaVA, MAVIS, MathCoder-VL: 이미지와 텍스트 정보를 잘 결합(alignment)하는 데 집중.
- Math-PUMA, URSA: 사람처럼 단계별 풀이 과정을 흉내내도록 설계.
- 강화학습(RL) 기반 접근
- 최근에는 모델이 단순히 정답을 맞히는 것보다, 복잡한 문제 풀이 과정을 잘 하도록 보상(Reward)을 최적화하는 연구들이 등장.
- 이런 RL 방법들이 실제로 모델의 복잡한 추론 능력을 높이는 데 성과를 보여주고 있습니다.
3 WE-MATH 2.0
WE-MATH 2.0은 멀티모달 대형 언어 모델(MLLMs)의 시각적 수학 추론 능력을 키우기 위해 설계된 통합 시스템입니다. 이 시스템은 세 가지 핵심 요소로 구성됩니다.
- MathBook Knowledge System (수학 지식 체계)
- 수학 개념을 5단계 계층으로 정리했습니다.
- 총 491개의 지식 포인트와 1,819개의 기본 원리를 포함해, 모델이 수학을 더 체계적이고 폭넓게 학습할 수 있도록 설계했습니다.
- 즉, “수학 백과사전” 같은 기반 지식을 모델에게 제공하는 역할을 합니다.
- Multi-Dimensional Data Construction (다차원 데이터 생성 파이프라인)
- 단순히 문제를 모으는 것이 아니라, 3단계 절차로 데이터를 만듭니다.
- Seed Problem Construction: 기초 문제를 만듭니다.
- Variant Expansion: 하나의 문제를 다양한 방식으로 변형시킵니다.
- 3차원 난이도 모델링: 난이도를 풀이 복잡성, 시각적 복잡성, 문맥 복잡성으로 나눠 체계적으로 문제를 난이도별로 구성합니다.
- 이를 통해 모델이 쉬운 문제에서 어려운 문제로 점진적으로 학습할 수 있게 됩니다.
- 단순히 문제를 모으는 것이 아니라, 3단계 절차로 데이터를 만듭니다.
- MathBookEval (평가 도구)
- 위에서 만든 지식 체계와 연결된 벤치마크(평가용 문제 세트).
- 모델이 단순히 정답을 맞히는 것뿐 아니라, 지식 포인트 전반에서 얼마나 균형 있게 추론할 수 있는지를 평가할 수 있도록 설계되었습니다.
3.1 MathBook Knowledge System
MathBook Knowledge System이란?
WE-MATH 2.0의 핵심 기초는 수학 지식을 체계적으로 정리한 5단계 계층 구조입니다.
- 기본 구조는 정의(Definition) → 정리(Theorem) → 응용(Application)이라는 교육 패러다임을 따릅니다.
- 여기에는 491개의 지식 포인트와, 그에 연결된 1,819개의 원리(정의·정리·응용)가 들어 있습니다.
- 즉, “수학 개념 → 관련 정리 → 실제 문제 적용”을 계층적으로 연결한 수학 지식 지도라고 보면 됩니다.
어떻게 만들었나? (Human–AI 협업)
- 사람 전문가가 초안 제작
- 교과서, 위키피디아, 국가 교육과정 같은 공신력 있는 자료를 기반으로 뼈대를 만듭니다.
- AI가 보조 참여
- 기존 수학 데이터셋(약 3만 문제)을 모아서 GPT-4o로 주제 태그를 붙입니다.
- 태그 간 의미 유사도를 분석해서 AI가 자동으로 계층 구조(Kauto)를 만듭니다.
- 최종 통합
- 전문가가 사람 버전(Khuman)과 AI 버전(Kauto)을 합치고, 품질 검토를 거쳐 최종 지식 체계 K를 완성합니다.
원리(Principle)까지 세밀하게 정리
- 문제 하나하나의 풀이 과정을 Chain-of-Thought(단계별 추론)에 따라 쪼개고, 각 단계가 어떤 지식 포인트에 해당하는지 매핑합니다.
- 예를 들어 문제 풀이가 “정의 → 피타고라스 정리 → 응용”이라면, 그 단계마다 관련 지식 포인트를 연결합니다.
- GPT-4o가 문제 풀이 과정에 사용된 정리·원리를 뽑아주면, 이를 모아서 각 지식 포인트가 어떤 원리 집합과 연결되는지 정리합니다.
- 마지막으로, 전문가가 이를 다시 검토·보완해서 완전하고 정확한 원리 집합(총 1,819개)을 구축합니다.
3.2 Multi-Dimensional Data Construction

3.2.1 MathBook-Standard: Seed and Variant Problem Construction
MathBook-Standard: 기본(seed) 문제와 변형(variant) 문제 만들기
1. Seed Problem Construction (기본 문제 만들기)
먼저, 지식 체계(MathBook Knowledge System)에 있는 개념과 원리에 맞게 "기본 문제"를 만듭니다. 여기에는 세 가지 원칙이 있습니다.
- 모든 도형은 GeoGebra라는 수학 전용 프로그램으로 정밀하게 그림을 그립니다.
- 문제는 수학적 본질에 집중하고, 그림의 단순한 특징(예: 색깔이나 위치) 같은 "겉모습 힌트"에 의존하지 않도록 합니다.
- 각 문제는 반드시 지정된 원리 집합(Pi)에 딱 맞도록 설계합니다.
구체적으로는,
- LLM이 초안 문제(문제·정답·도형 스크립트)를 만듭니다.
- GeoGebra가 이 스크립트를 읽어 "임시 도형"을 자동 생성합니다.
- 이걸 바탕으로 전문가가 직접 문제와 그림을 수정·보완해서 최종 버전 문제를 만듭니다.
이렇게 해서 모든 지식 포인트(491개)와 원리(1,819개)를 커버하는 기본 문제 세트가 완성됩니다.
2. Variant Problem Expansion (문제 변형 만들기)
기본 문제 하나로 끝내지 않고, 더 다양한 버전을 만들어 모델이 더 잘 일반화할 수 있도록 합니다. 두 가지 방식이 있습니다.
① 한 문제 → 여러 그림 (One-Problem-Multi-Image)
- 문제 내용은 그대로 두고, 도형만 다르게 만듭니다.
- 예: "삼각형의 각을 구하라"라는 같은 문제를, 예각삼각형·둔각삼각형·직각삼각형 등으로 변형합니다.
- 그림이 달라지면 답도 달라지지만, 문제의 원리는 같습니다.
② 한 그림 → 여러 문제 (One-Image-Multi-Problem)
- 같은 도형을 두고, 다른 질문을 냅니다.
- 예: 같은 원의 그림에서
- 원의 반지름을 구하라
- 현의 길이를 구하라
- 중심각의 크기를 구하라
같은 식으로 여러 문제를 만들 수 있습니다.
3.2.2 MathBook-Pro: Three-Dimensional Difficulty Modeling
MathBook-Pro란?
MathBook-Standard가 "다양한 문제집"이라면,
MathBook-Pro는 난이도를 체계적으로 조절한 고급 문제집입니다.
핵심 아이디어는 난이도를 3가지 축으로 나눠서 설계한다는 것인데, 이는 모델 중심 관점에서 "얼마나 어려운가?"를 정량적으로 정의하려는 시도입니다.
난이도 3차원 축 (Three-Dimensional Difficulty Space)
- Step Complexity (풀이 단계 복잡성, ϕs)
- 문제를 푸는 데 필요한 지식 포인트 개수로 난이도를 조절합니다.
- 예:
- 쉬운 문제: “피타고라스 정리” 하나만 쓰면 됨
- 어려운 문제: “삼각비 + 피타고라스 정리 + 원주각 정리 + 방정식” 같이 여러 개념을 연달아 써야 함
- MathBook-Pro에서는 가장 어려운 경우, 최소 6개 이상의 지식 포인트를 써야 풀리도록 설계했습니다.
- Visual Complexity (시각적 복잡성, ϕv)
- 그림을 더 복잡하게 만듭니다.
- 예: 삼각형 문제에 보조선, 추가 점, 새로운 도형 요소를 넣어서 난이도를 높입니다.
- 단, 원래 구조는 유지하면서 시각적인 부담을 늘립니다.
- Contextual Complexity (문맥적 복잡성, ϕc)
- 문제 설명을 더 복잡하게 만듭니다.
- 예:
- 단순 버전: “삼각형의 넓이를 구하라”
- 복잡 버전: “한 농부가 땅을 세 개 구역으로 나눴는데, 각각의 구역은 삼각형 모양이며, 그중 하나의 넓이를 구하라”
- 즉, 수학적 본질은 같지만, 현실 맥락이나 언어적 장치를 덧붙여 문제를 더 어렵게 만듭니다.
어떻게 문제를 만드는가?
- 모든 기본 문제(seed problem)는 (문제 q₀, 답 a₀, 그림 I₀)에서 시작합니다.
- 여기서 한 번에 한 가지 축(ϕs, ϕv, ϕc)만 바꿔서 변형 문제를 만듭니다.
- 예: 같은 삼각형 문제 → (1) 지식 단계 추가, (2) 그림에 보조선 추가, (3) 문맥 복잡화
- 이렇게 여러 번 단계를 쌓아가면, 세 축이 합쳐져 최종적으로 가장 어려운 버전을 만듭니다.
결과
- MathBook-Pro는 문제를 난이도별로 세밀하게 통제할 수 있습니다.
- 각 지식 포인트마다, 쉬운 버전부터 고난도 버전까지 일관된 계열이 생깁니다.
- 이렇게 해서 Ddifficulty라는 난이도 모델링 전용 하위 데이터셋이 구축됩니다.
3.3 MathBookEval
MathBookEval이란?
MathBookEval은 모델의 수학 추론 능력을 제대로 평가하기 위해 만든 새로운 벤치마크(평가용 문제 세트)입니다. 기존 벤치마크보다 훨씬 더 폭넓고 체계적으로 설계되었습니다.
설계 원칙 (Design Principles)
- 폭넓은 지식 커버리지
- 초등학교부터 대학교 수학까지, 총 491개의 지식 포인트를 다룹니다.
- 즉, 특정 분야에 치우치지 않고 전체 수학 영역을 포함합니다.
- 깊이 있는 추론 평가
- 문제마다 필요한 지식 포인트 개수를 1~10개로 다양화했습니다.
- 기존 벤치마크는 보통 1~3개만 요구했는데, 여기서는 단계적으로 더 깊은 추론(최대 10단계)을 확인할 수 있습니다.
- 철저한 주석(Annotation) 과정
- 기존 문제와 새로 만든 문제를 하나의 기준으로 통합합니다.
- 전문가가 문제 풀이 과정을 단계별로 직접 표시하고, 각각을 어떤 지식 포인트에 해당하는지 명확히 연결합니다.
- 서로 다른 사람이 교차 검증(cross-validation)해서 일치하는 문제만 최종 채택 → 품질 보장.
데이터 구성 (Data Statistics)
- 총 1,000문제
- 600개는 기존 벤치마크에서 가져온 문제
- 400개는 새로 만든 문제
- 두 가지 기준으로 나눠서 관리합니다.
- Reasoning Dimension (추론 깊이)
- Level 1: 1~3단계 추론
- Level 2: 4~6단계 추론
- Level 3: 7~10단계 추론
→ 문제 난이도를 추론 단계 수로 체계적으로 나눔
- Knowledge Dimension (지식 영역)
- 491개 지식 포인트를 4개 대분야, 13개 세부 분야로 그룹화
- 기초부터 고급 수학까지 모두 포함
- Reasoning Dimension (추론 깊이)
- 문제 형식은 객관식이나 단답형(빈칸 채우기) 방식으로 되어 있습니다.
4 Methodology
MathBook-RL이란?
MathBook-RL은 멀티모달 언어모델(MLLMs)이 수학 추론을 단계적으로 잘하게 만드는 훈련 방법입니다.
훈련은 두 단계로 나뉩니다.
- Cold-Start Fine-Tuning (초기 파인튜닝 단계)
- 모델이 처음부터 바로 어려운 문제를 풀 수 없으니,
- 지식 기반의 풀이 방식(Chain-of-Thought reasoning)을 먼저 익히도록 합니다.
- 즉, 모델에게 “문제를 풀 때는 개념 → 정리 → 풀이 단계 순으로 생각해야 한다”는 기본 추론 패턴을 심어주는 단계입니다.
- Dynamic Reinforcement Learning (동적 강화학습 단계)
- 그다음에는 강화학습(RL)을 이용해 쉬운 문제 → 점점 어려운 문제로 확장하며 훈련시킵니다.
- 이 과정에서 모델은 단순히 배운 문제를 외우는 것이 아니라, 새로운 문제에도 일반화 능력을 발휘할 수 있게 됩니다.
4.1 Cold-Start Fine-tuning
Cold-Start Fine-tuning이란?
이 단계는 모델에게 “수학을 단순히 외우지 말고, 지식 체계에 따라 사고하면서 풀어라”라는 습관을 심어주는 초기 학습 과정입니다.
구체적으로 어떻게 하나?
- 학습 데이터 준비 (Dinit)
- MathBook-Standard 데이터셋을 사용 → 491개 모든 지식 포인트가 포함됨.
- 즉, 수학 전 영역을 빠짐없이 커버하는 기본 문제들을 사용합니다.
- 문제 재작성 (자연어 설명 추가)
- 단순히 문제와 정답만 주는 게 아니라,
- GPT-4o를 이용해 문제 풀이 과정을 자연어로 풀어서 설명합니다.
- 이때 “이 문제는 피타고라스 정리를 사용해야 한다”처럼, 관련 지식 포인트를 명시적으로 언급하도록 만듭니다.
- 지도학습(SFT) 진행
- 이렇게 준비된 데이터를 이용해 모델을 슈퍼바이즈드 파인튜닝(지도학습)으로 학습시킵니다.
- 즉, 입력(x, 문제) → 출력(y, 풀이·정답)을 모델이 잘 예측하도록 훈련.
결과
- 모델이 단순히 정답만 외우는 게 아니라,
- “문제를 보면서 → 관련 개념을 떠올리고 → 단계적으로 추론하는 습관”을 가지게 된다.
- 즉, 지식 체계에 기반한 논리적 풀이 과정(Reasoning Chain)을 내재화하게 된다.
4.2 Progressive Alignment Reinforcement Learning
전체 그림
Cold-start 단계에서 모델이 “개념을 근거로 단계별로 생각하는 습관”을 배웠다면, 이제 Progressive Alignment RL에서는 쉬운 문제 → 어려운 문제로 점차 확장하면서 강화학습으로 훈련시킵니다.
즉, 학생에게 기초 개념을 가르친 뒤, 점점 더 어려운 문제를 단계별로 풀게 만드는 과정이라고 볼 수 있습니다.
1) Pre-aligned RL (사전 정렬 학습)
- MathBook-Standard 데이터셋을 활용해 먼저 강화학습을 합니다.
- 특히 DImgVar (같은 원리, 다른 그림 버전 문제 모음)을 사용합니다.
- 예: 같은 “피타고라스 정리” 문제를 직각삼각형, 둔각삼각형, 예각삼각형 등 다양한 그림으로 변형.
- 보상 방식
- 답이 맞으면 0.9점
- 답은 틀렸지만 형식만 맞으면 0.1점
- 둘 다 틀리면 0점
- 즉, 같은 지식 원리 문제에서 다양한 변형에도 일관성 있게 잘 푸는지를 강화학습으로 다집니다.
2) Dynamic Scheduling RL (동적 스케줄링 학습)
이제 MathBook-Pro (난이도 조절된 문제집)를 이용해 점진적으로 난이도를 올립니다.
- 기본 흐름:
쉬운 문제 (x0) → 단계 복잡성 추가 (ϕs) → 단계 + 시각 복잡성 (ϕs◦ϕv) → 단계 + 문맥 복잡성 (ϕs◦ϕc) → 단계 + 시각 + 문맥 복잡성 (ϕs◦ϕv◦ϕc)
- 즉, 한 문제를 “지식 더 필요 → 그림 더 복잡 → 언어 문맥 더 까다롭게” 순서로 점진적으로 강화합니다.
3) Incremental Learning (증분 학습 메커니즘)
만약 모델이 어려워진 단계에서 틀리면, 바로 포기하지 않고 중간 단계용 보충 문제를 줍니다.
- Knowledge Increment Scheduling
- 새로운 지식 포인트 때문에 틀렸으면 → 그 지식 포인트만 따로 연습 문제 제공
- Modality Increment Scheduling
- 그림(시각)이나 언어(문맥) 복잡성 때문에 틀렸으면 → 그 요소만 따로 간단한 연습 문제 제공
즉, 모델이 어려움에 막히면 필요한 부분만 따로 보충학습을 해서 다시 시도하게 만듭니다.
4) 최종 목표
- 이 과정은 GRPO(Group Relative Policy Optimization)라는 강화학습 기법으로 최적화됩니다.
- 기존 PPO(정책 최적화)의 변형으로, 개별 문제 대신 문제 그룹 단위로 보상을 평가해 안정성을 높입니다.
결과
이 방식 덕분에 모델은
- 단순히 정답을 맞히는 데 그치지 않고,
- 지식(수학 개념), 시각(복잡한 그림), 문맥(복잡한 설명)이 모두 결합된 어려운 문제도 점진적으로 익힐 수 있습니다.
- 따라서 일관성, 일반화 능력, 복잡한 추론 능력이 함께 향상됩니다.
5 Experiments
5.1 Experimental Setup
데이터셋
- 모든 훈련 데이터는 WE-MATH 2.0에서 만든 것만 사용 (저작권 문제 없음).
- 사용된 데이터 규모
- 1K (1천 개) → Cold-start 파인튜닝(SFT)
- 5.8K (5천8백 개) → Pre-aligned RL
- 4K (4천 개) → Dynamic Scheduling RL
- 평가 벤치마크는 수학 추론에서 널리 쓰이는 4가지
- MathVista, MathVision, MathVerse, We-Math
비교 대상 (Baselines)
- 실험 모델은 Qwen2.5-VL-7B 기반으로 학습.
- 비교 그룹은 3가지로 나눔
- 비공개 모델: GPT-4o
- 오픈소스 범용 모델: InternVL2.5, Qwen2.5-VL 시리즈
- 오픈소스 추론 특화 모델: R1-VL
- 성능 평가는 VLMEvalKit 도구 사용 (네트워크 제약 때문에 일부 수정).
5.2 Main Results
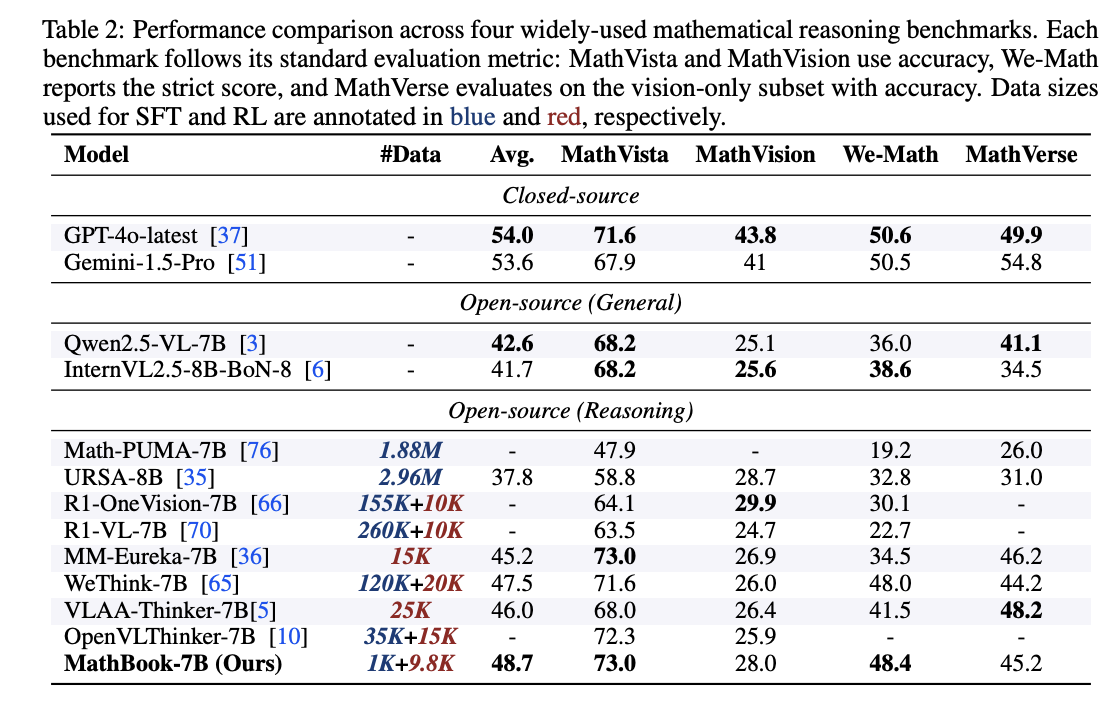
실험 결과, MathBook-7B 모델이 모든 벤치마크에서 눈에 띄게 좋은 성능을 보였다. 주요 관찰점은 다음과 같습니다
- 전반적 성능 향상
- 기본 모델(Qwen2.5-VL-7B)보다 모든 벤치마크에서 +5% 이상 성능 향상.
- 이는 MathBook 접근법의 효과성을 검증한 것.
- 지식 일반화 효과 (Progressive RL의 강점)
- 특히 We-Math 벤치마크에서 큰 효과를 보임.
- 이 벤치마크는 "복잡한 다단계 문제"와 "그 문제의 하위 문제"를 모두 풀 수 있어야 하는데,
- MathBook-7B는 기존의 강화학습(RL) 기반 모델보다 뛰어난 성능을 보였습니다.
- 즉, 점진적 강화학습(Progressive RL)이 지식 일반화에 효과적이라는 것을 입증.
- 적은 데이터로도 높은 성능 (Less is More)
- 주목할 점: MathBook-7B는 훈련 샘플이 9.8K(약 1만 개 미만) 밖에 안 되는데도 강력한 성능을 발휘.
- 이는 우리가 만든 체계적이고 고품질의 수학 지식 시스템 덕분에,
데이터가 많지 않아도 효율적으로 학습하고 일반화할 수 있었음을 보여줍니다.
5.3 Results on MathBookEval
- 추론 단계가 많아질수록 성능 저하
- 필요한 지식 포인트 개수가 늘어날수록 모델 정확도는 꾸준히 떨어짐.
- 특히 7~10단계 추론이 필요한 문제에서는 대부분 정확도가 50% 미만.
- → 여전히 다단계 추론(multi-step reasoning)이 가장 큰 난관임을 확인.
- 대수(Algebra)는 잘하지만, 기하(Geometry)는 약함
- 대수 문제에서는 정확도 50% 이상으로 꽤 좋은 성과.
- 하지만 기하학 문제(도형, 공간 추론)에서는 성능이 일관되게 낮음.
- → MLLMs가 공간적 추론(spatial reasoning)에 약하다는 기존 문제를 다시 확인.
- 모델 크기가 클수록 성능이 꾸준히 향상됨
- InternVL2.5, Qwen2.5-VL 계열에서 모델 크기가 커질수록 모든 영역에서 성능 향상이 나타남.
- → 스케일(Scale)이 수학 추론 능력을 높이는 중요한 요인임을 보여줌.
Ablation Study (M0~M4 실험 비교, Table 3)

- M0 (SFT + RL-Pre + RL-Dyn): 성능 최고 (MathVista 73.0, MathVision 28.0, We-Math 48.4)
- 일부 단계를 뺄수록 점수 하락
- RL-Dyn을 빼면 하락 (M1)
- RL-Pre를 빼도 하락 (M2)
- SFT를 빼도 하락 (M3)
- 둘 다 빼면 최악 (M4: We-Math 38.3)
- → Cold-Start SFT, RL-Pre, RL-Dyn 세 단계가 모두 필요함을 입증.
5.4 Quantitative Analysis
SFT Data Paradigm & Scale 분석

이번엔 SFT 단계에서 데이터 형식과 데이터 크기가 성능에 어떤 영향을 주는지 확인했습니다.
주요 발견 두 가지
- 자연어 CoT(Chain-of-Thought)가 더 효과적이다
- 자연어로 설명된 CoT vs 구조적 단계별 CoT(Structured Format)를 비교.
- 결과: 자연어 CoT가 더 좋은 성능을 냄.
- → 자연스러운 언어 설명이 모델의 유연한 추론 능력을 키워주고, 시각적 수학 추론까지 강화한다는 의미.
- SFT는 "작고 고품질"이면 충분하다
- SFT 데이터를 1K → 10K로 늘려도 성능이 크게 오르지 않음.
- 오히려 잘 정제된 소량의 데이터로 학습한 모델이 더 안정적이거나 성능이 더 좋음.
- → 즉, SFT는 대규모 데이터보다는 소량의 고품질 데이터가 핵심.
정리
- 훈련 단계별 역할
- SFT: 혼자서는 성능 제한적 → 하지만 RL 효과를 끌어내는 "시동 장치"
- RL-Pre: 수학 지식 기반 강화학습 → 복잡 문제 일반화에 효과
- RL-Dyn: 난이도 점진적 강화학습 → 어려운 문제 적응에 효과
- 데이터 관련 통찰
- 자연스러운 언어(CoT) 설명이 구조적 설명보다 모델 추론 능력 향상에 더 좋음
- SFT는 많을 필요 없음 → 적더라도 고품질이면 충분
6 Conclusion
이 논문에서는 WE-MATH 2.0이라는 멀티모달 수학 추론용 통합 프레임워크를 제안했다. 이 시스템은 네 가지 주요 구성 요소로 이루어져 있습니다.
- MathBook Knowledge System
- 5단계 계층 구조로 정리된 수학 지식 체계
- 491개의 지식 포인트와 1,819개의 원리 포함
- 모델이 체계적으로 수학 지식을 배울 수 있도록 감독(supervision) 제공
- MathBook-Standard & MathBook-Pro (데이터셋)
- MathBook-Standard: 개념 확장(문제-그림 변형 등)으로 풍부하게 구성된 문제집
- MathBook-Pro: 난이도를 3차원(풀이 단계, 시각 복잡성, 문맥 복잡성)으로 모델링한 고급 문제집
- → 체계적이고 점진적인 학습 가능
- MathBook-RL (강화학습 프레임워크)
- 두 단계로 구성
- Cold-start SFT → 지식 기반 추론 패턴 학습
- Progressive RL → 난이도 점진적 강화, 일반화 능력 강화
- 지식·시각·문맥 난이도를 조절하며 모델이 단계적으로 성장하도록 훈련
- 두 단계로 구성
- MathBookEval (평가 도구)
- 모든 지식 포인트와 다양한 풀이 깊이를 커버하는 평가 세트
- 모델의 추론 능력과 일반화 성능을 체계적으로 검증
최종 결론
광범위한 실험 결과, WE-MATH 2.0은 멀티모달 대형 언어모델(MLLMs)의 수학적 추론 능력을 크게 개선했으며, 특히 일반화 능력을 강화하는 데 효과적임이 입증되었습니다.


댓글