ProtoReasoning: Prototypes as the Foundation forGeneralizable Reasoning in LLMs

원문: https://arxiv.org/pdf/2506.15211

 

Abstract

AI가 추론을 더 잘하도록 만드는 새로운 방법을 제안하는 논문

 

핵심 아이디어: AI가 서로 다른 분야의 문제를 잘 푸는 이유는 모든 문제 뒤에 공통된 "추론 패턴"이 있기 때문

ProtoReasoning 방법

1. 문제를 간단한 형태로 변환: 복잡한 자연어 문제를 Prolog나 PDDL 같은 컴퓨터가 이해하기 쉬운 형태로 바꿉니다
2. 자동 검증: 답이 맞는지 컴퓨터가 자동으로 확인해줍니다
3. 무한 확장: 이 방식으로 새로운 문제를 계속 만들어냅니다

결과

• 논리 추론: 4.7% 향상
• 계획 수립: 6.3% 향상
• 일반 추론: 4.0% 향상
• 수학: 1.0% 향상

기여점: AI가 단순히 암기가 아니라 진짜 "추론 패턴"을 학습하게 되어, 새로운 종류의 문제도 더 잘 풀 수 있게 된다는 것을 보여줍니다.

1 Introduction

AI가 한 분야(예: 수학)에서 배운 추론 능력을 다른 분야(예: 글쓰기)에서도 잘 쓸 수 있다는 게 관찰되었는데, 왜 그런지 모르겠더라는 것이다!

가설: "서로 다른 문제들도 실제로는 비슷한 '추론 구조'를 가지고 있어서 그런 거 아닐까?"

해결 방법 - ProtoReasoning

1. 문제를 단순한 형태로 변환
   • 복잡한 자연어 문제를 Prolog(논리용)나 PDDL(계획용) 같은 컴퓨터 언어로 바꿈
2. 자동 검증
   • 답이 맞는지 컴퓨터가 자동으로 확인
   • 사람이 일일이 채점할 필요 없음
3. 무한 확장
   • 한 번 "문제 틀"을 만들면, 그 틀로 비슷한 구조의 새 문제를 계속 자동 생성
   • 사람이 문제-답 쌍을 만들 필요 없이, 컴퓨터가 문제를 만들고 답도 자동으로 계산

2 The ProtoReasoning Framework

2.1 Overview

ProtoReasoning은 두 개의 핵심 모듈로 이루어져 있음

 

• 프로토타입 생성기: 문제를 해당 프로토타입 표현으로 변환하는 모듈
• 검증 시스템: 프로토타입 표현 공간에서 모델 출력의 정확성을 평가하는 모듈

 

2.2 Logic Prototype Representations

rolog(논리 프로그래밍)는 1차 술어 논리에 기반한 선언적 언어로, 통합과 백트래킹 메커니즘을 사용하여 논리 문제를 표현하고 해결합니다. 선언적 특성으로 인해 절차적 알고리즘이 아닌 논리적 제약으로 문제를 표현할 수 있어 인간의 추론 패턴과 자연스럽게 대응됩니다. LLM이 Prolog로 공식화된 문제를 해결하도록 훈련시킴으로써, 다양한 문제 도메인에서 기본적인 논리적 추론 능력을 체계적으로 향상시킵니다.

2.2.1 Prolog-based Logic Prototype Constructor

다양하고 검증 가능한 Prolog 추론 문제를 생성하기 위해 4단계 모델 중심 파이프라인을 설계했습니다

1. 데이터 초기화: 웹 소스에서 구조화된 질문-답변 쌍과 비구조화된 논리적 서술을 모두 포함하는 포괄적인 추론 문제 말뭉치를 수집했습니다.
2. 프로토타입 변환: LLM과의 프롬프트 엔지니어링을 통해 자연어 논리 문제를 공식적인 Prolog 표현으로 변환하고, 해석기 출력을 구조화된 JSON 형식으로 표준화했습니다.
3. 데이터 진화: 프롬프트 엔지니어링을 활용하여 JSON 출력 제약을 유지하면서 제어 가능한 방식으로 문제 복잡성을 체계적으로 향상시켰습니다.
4. 답안 도출: SWI-Prolog 해석기를 사용하여 정답을 도출했습니다. 이러한 해석기 기반 접근법은 기존 질문-답변 쌍에 대한 의존성을 제거하고 답안 부정확성을 도입하지 않으면서 문제 난이도를 자신 있게 발전시킬 수 있게 합니다.

2.2.2 Prolog-based Verification System

앞 섹션에서 설명한 프로토타입 변환을 바탕으로, 모든 참조 답변 A를 구조화된 JSON 딕셔너리로 제한했습니다. 그런 다음 모델이 동일한 JSON 형식으로 예측 Aˆ를 생성하도록 지시하는 훈련 프롬프트 템플릿을 개발했습니다. 이러한 표준화는 Prolog 해석기의 출력과 모델 예측 간의 엄격한 평가를 용이하게 하여 둘 다 일관된 형식으로 표현되도록 보장합니다.

2.3 Planning Prototype Representations

PDDL(계획 도메인 정의 언어)은 자동 계획 문제의 표준 표현으로, 상태 표현, 전제조건과 효과가 있는 행동, 상태 전이라는 세 가지 필수 구성요소를 통해 상태 전이 시스템을 모델링합니다. 이 표현은 특히 행동 요구사항과 결과에 대한 추론에서 인간의 계획 인지와 자연스럽게 일치합니다.

2.3.1 PDDL-based Planning Prototype Constructor

계획 작업을 위해 PDDL-Generator와 FastDownward를 사용하여 다양한 도메인에서 문제를 생성하고 최적 해답을 도출했습니다. 국제 계획 경쟁(IPC) 벤치마크를 기반으로 BlocksWorld와 Logistics 같은 고전적 도메인에서 다양한 복잡성의 문제를 생성했습니다. 각 도메인에 대해 세 가지 구별되는 작업 유형을 구성했습니다.

1. 계획 생성: 도메인 정의와 문제 기술이 주어졌을 때, 모델은 초기 상태에서 목표 상태까지의 완전한 행동 순서를 생성해야 하며, 종단간 계획 능력을 테스트합니다.
2. 계획 완성: 부분적인 행동 순서가 제공되었을 때, 모델은 누락된 단계를 채워야 하며, 중간 상태에 대한 이해와 양방향 추론이 필요합니다.
3. 계획 재정렬: 순서가 없는 행동 단계가 주어졌을 때, 모델은 유효한 실행 순서를 결정해야 하며, 행동 의존성과 전제조건 관계에 대한 이해를 테스트합니다.

2.3.2 PDDL-based Verification System

정확한 JSON 딕셔너리 비교에 의존하는 Prolog 검증과 달리, PDDL 작업은 동일한 문제에 대해 여러 유효한 계획이 존재할 수 있으므로 전문적인 검증이 필요합니다. VAL(PDDL 계획 검증기)을 활용하여 각 작업 유형에 대한 맞춤형 검증 절차를 구현했습니다.

1. 계획 생성: 표준 생성 작업의 경우, VAL 검증을 통과하는 모든 계획을 정확한 것으로 받아들이며, 참조 값이 필요하지 않습니다. 계획 비용이 중요한 최적화 작업(최소 또는 최대 비용 계획)의 경우, FastDownward 솔버를 사용하여 참조 최적 값을 설정합니다.
2. 계획 완성: 여기서 Pref는 주어진 부분 계획을 포함합니다. 모델의 출력은 VAL 검증을 통과하면서 부분 계획의 모든 행동을 정확한 위치에 포함해야 합니다.
3. 계획 재정렬: 이 경우 Pref는 순서가 없는 행동 단계를 포함합니다. 올바른 해답은 VAL 검증을 통과하고 Pref에 지정된 것과 동일한 행동 집합을 포함해야 합니다 — 누락된 행동이나 추가 행동이 없어야 합니다.

2.4 Model Training Recipe

이 섹션에서는 효과성을 검증하기 위해 지도 미세조정을 활용하는 3단계 훈련 접근법을 소개합니다.

1. 교사 모델 증류: 고성능 언어 모델인 Deepseek-R1을 사용하여 초기 데이터셋에 대한 명시적 추론 체인을 생성했습니다. 이 변환은 단계별 추론 경로를 포함하도록 데이터를 풍부하게 만들어, Prolog 작업을 위한 증강 데이터셋과 PDDL 작업을 위한 증강 데이터셋을 생성했습니다.
2. 난이도 계층화: 이전 단계에서 훈련된 모델을 사용하여 거부 샘플링 방법론을 구현하여 인스턴스를 난이도별로 분류합니다. 각 문제를 10번 평가하고 통과율에 따라 분류합니다.
   • 도전적: 0 < 통과율 ≤ 0.3
   • 중간: 0.4 ≤ 통과율 ≤ 0.6
   • 초급: 0.7 ≤ 통과율 < 1

완전히 해결된 인스턴스(통과율 = 1.0)와 완전히 실패한 것들(통과율 = 0)을 모두 제외하고, 이 계층화된 데이터셋으로 향상된 모델을 훈련합니다.

3. 품질 필터링: 두 번째 단계의 정제된 모델로 최종 거부 샘플링을 수행하여 최종 훈련 데이터셋을 생성합니다.

3 Experiments

3.1 Experimental Setup

데이터 준비

• 기본: 100,000개의 다양한 문제들
• 새로 만든 것: Prolog 4,196개 + PDDL 2,424개 (원래 77,000개에서 걸러낸 것)

테스트 방법

• 논리 테스트: Enigmata-Eval (단순한 지시 따르기 문제는 제외)
• 계획 테스트: 직접 계획 문제 + 함수 호출 문제 (둘 다 순서대로 뭔가 해야 하는 공통점)
• 일반화 테스트: MMLU (상식) + AIME24 (수학) - 원래 배우지 않은 분야

모델: 150B 총 매개변수에서 15B 매개변수를 활성화하는 Mixture-of-Experts(MoE) 아키텍처를 훈련 모델로 채택했습니다. 훈련은 2e-5의 학습률과 시퀀스 패킹이 활성화된 배치 크기 6을 사용했습니다.

3.2 Experimental Results

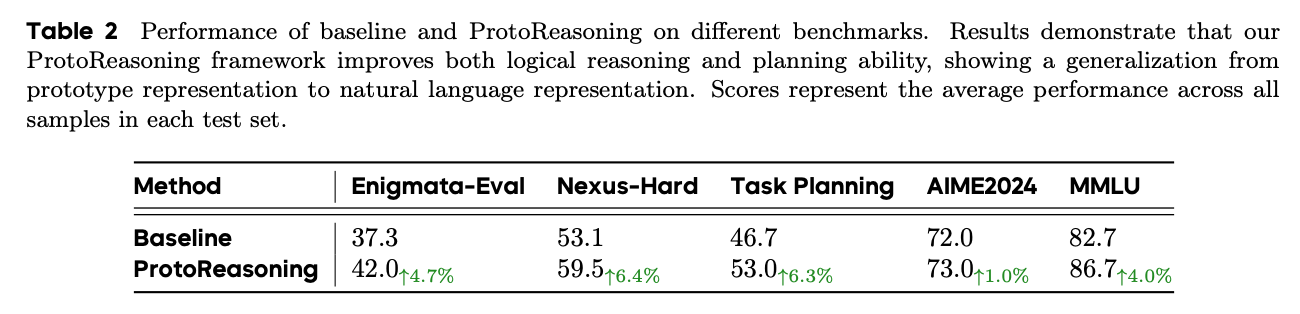
결과 요약

• 논리 추론: 37.3% → 42.0% (+4.7%)
• 계획 수립: 53.1% → 59.5% (+6.4%), 46.7% → 53.0% (+6.3%)
• 일반 상식: 82.7% → 86.7% (+4.0%)
• 수학: 72.0% → 73.0% (+1.0%)

AI가 Prolog와 PDDL로 훈련받으니까 원래 배운 논리/계획뿐 아니라 전혀 다른 분야(상식, 수학)에서도 더 잘하게 되었음!

3.3 Ablation Study

비교 분석 설정: Enigmata-Eval 벤치마크를 별개의 훈련 및 개발 세트로 분할했습니다. 훈련 부분집합을 두 가지 방법으로 처리했습니다. (1) 해석기로 검증된 해답과 함께 Prolog 표현으로 변환

(2) Enigmata-Eval의 기본 검증기로 검증된 다단계 거부 샘플링을 활용한 원래 자연어 문제 준비. 이 절차는 453개 샘플의 매칭된 훈련 말뭉치를 생성했으며, 이는 Prolog와 자연어 형식 모두로 인코딩된 문제들의 교집합을 나타냅니다.

 

세 가지 실험 구성을 설계함

1. 기준선 (방법 1): 표준 데이터셋에서만 훈련된 모델
2. 기준선 + Prolog 표현 (방법 2): Enigmata 추론 문제의 공식화된 Prolog 표현으로 보강된 표준 데이터셋으로 훈련된 모델
3. 기준선 + 자연어 (방법 3): 프로토타입 접근법에서 사용된 동일한 추론 문제의 자연어 버전으로 보강된 표준 데이터셋으로 훈련된 모델

비교 분석 평가: 추론 전이의 다양한 측면을 평가하기 위해 두 가지 상호 보완적인 테스트 세트를 사용

1. 프로토타입 전이 세트: Prolog 훈련 예제를 만드는 데 사용된 Enigmata-Eval 문제들의 원래 자연어 버전
2. 개발 세트: 프로토타입 전이 세트를 만드는 데 사용되지 않은 Enigmata-Eval의 나머지 부분

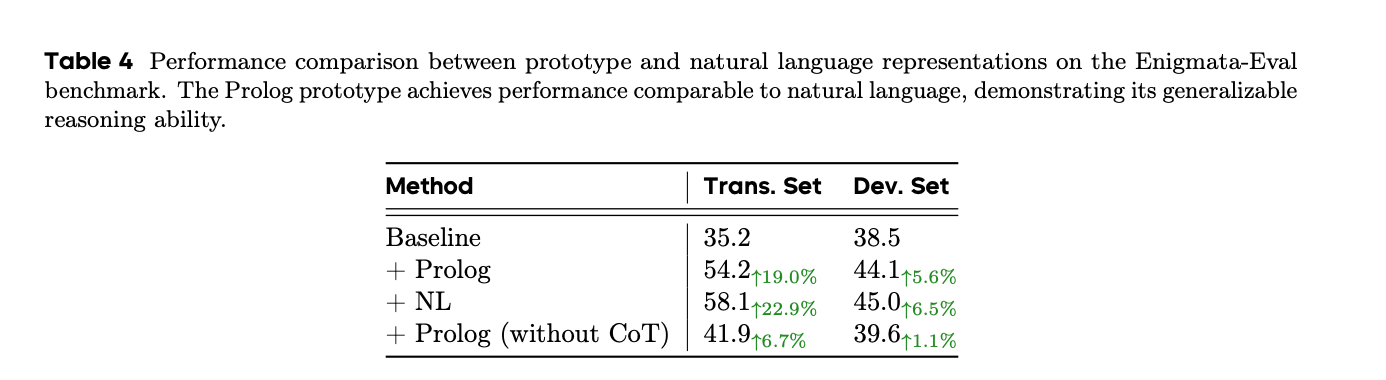
결과 및 분석: 표 4는 Prolog 표현이 전이 세트와 개발 세트 모두에서 상당하고 일관된 성능 향상을 가져온다는 것을 보여줍니다. 기준선에 대한 기준선 + Prolog 표현(방법 2)의 성능 향상은 프로토타입 표현에서의 훈련이 자연어 문제로 효과적으로 일반화된다는 것을 검증합니다.

더욱이, 방법 2(Prolog 표현 사용)와 방법 3(자연어 사용) 간의 비교 가능한 성능은 프로토타입 훈련이 직접적인 자연어 훈련과 유사한 효과를 달성한다는 것을 확인하며, 프로토타입의 일반화 보여줍니다

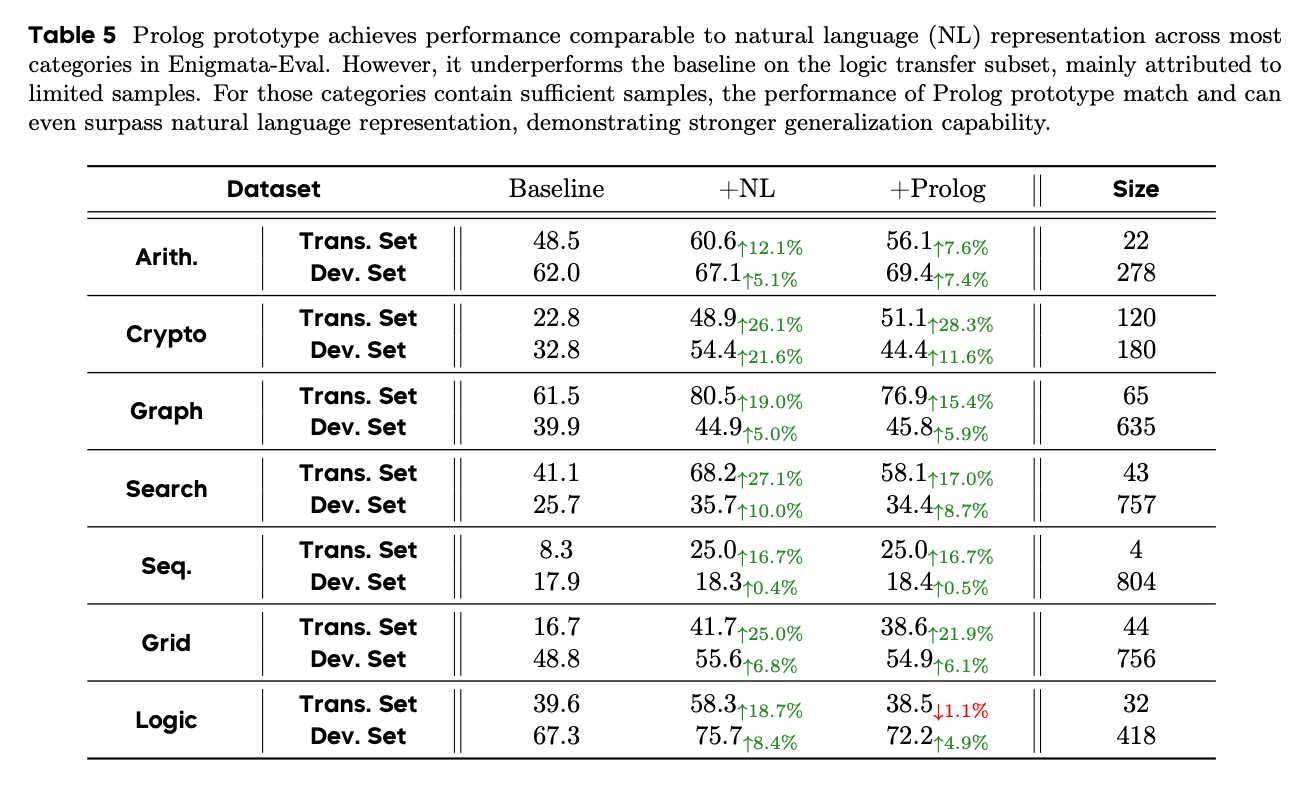
4 Related Work

최근 AI 추론 발전 동향

• 과거: CoT(사고의 연쇄) + 지도학습 
• 현재: 강화학습 중심

대표적인 모델들

• DeepSeek-R1: 수학, 코딩으로 긴 추론 연습
• Logic-RL: 논리 퍼즐로 수학까지 잘하게 됨
• 공통점: 검증 가능한 보상(맞으면 +점수)으로 강화학습

이 연구들의 성과

• 실수를 스스로 찾아 고치기
• 어려운 문제를 작은 단계로 나누기
• 여러 방법을 시도해보기
• → 한 분야에서 배운 걸 다른 분야에 잘 적용하기

5 Conclusion and Future Work

연구에서 이룬 것

• ProtoReasoning 프레임워크 개발: Prolog(논리용) + PDDL(계획용)으로 AI 훈련
• 가설 증명: "서로 다른 문제들도 공통된 추론 패턴이 있다"는 걸 실험으로 확인
• 성과: 논리, 계획뿐 아니라 상식, 수학까지 모든 분야에서 성능 향상
• 일반화 가능성: 다른 AI 능력(언어, 창작 등)에도 이 방법 적용 가능할 듯

한계

• 이론적 한계: "추론 프로토타입"이 정확히 뭔지 수학적으로 명확하게 정의 못함
• 메커니즘 불명: 왜 이게 작동하는지 근본 원리를 완전히 이해하지 못함
• 좀 더 엄밀한 수학적 증명이 필요해요

향후 연구

1. 수학적 이론 개발: "추론 프로토타입"을 수학으로 정확히 정의하고 증명
2. 데이터 공개: 우리가 만든 Prolog, PDDL 데이터셋을 연구자들에게 무료 제공
3. 오픈소스 검증: 다른 AI 모델들에서도 같은 결과가 나오는지 확인