한빛미디어에서 모집하는 혼공학습단 활동의 일환으로 혼자 공부하는 머신러닝+딥러닝 책을 공부하고 정리한 글입니다. 책은 제 돈으로 구매했습니다. 원본 코드는 저자 박해선 님의 깃허브에서 보실 수 있습니다.
GitHub - rickiepark/hg-mldl: <혼자 공부하는 머신러닝+딥러닝>의 코드 저장소입니다.
<혼자 공부하는 머신러닝+딥러닝>의 코드 저장소입니다. Contribute to rickiepark/hg-mldl development by creating an account on GitHub.
github.com
Chapter 06 비지도 학습
06-1 군집 알고리즘
타깃을 모르는 비지도 학습
| 비지도 학습 unsupervised learning 타깃이 없을 때 사용하는 머신러닝 알고리즘 |
과일 사진 데이터 준비하기
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
import matplotlib.pyplot as plt
fruits = np.load('fruits_300.npy')
print(fruits.shape)
print(fruits[0, 0, :])
plt.imshow(fruits[0], cmap='gray')
plt.show()
plt.imshow(fruits[0], cmap='gray_r')
plt.show()
fig, axs = plt.subplots(1, 2)
axs[0].imshow(fruits[100], cmap='gray_r')
axs[1].imshow(fruits[200], cmap='gray_r')
plt.show()
픽셀값 분석하기
apple = fruits[0:100].reshape(-1, 100*100)
pineapple = fruits[100:200].reshape(-1, 100*100)
banana = fruits[200:300].reshape(-1, 100*100)print(apple.shape)
print(apple.mean(axis=1))
| 히스토그램 값이 발생한 빈도를 그래프로 표시한 것 |
plt.hist(np.mean(apple, axis=1), alpha=0.8)
plt.hist(np.mean(pineapple, axis=1), alpha=0.8)
plt.hist(np.mean(banana, axis=1), alpha=0.8)
plt.legend(['apple', 'pineapple', 'banana'])
plt.show()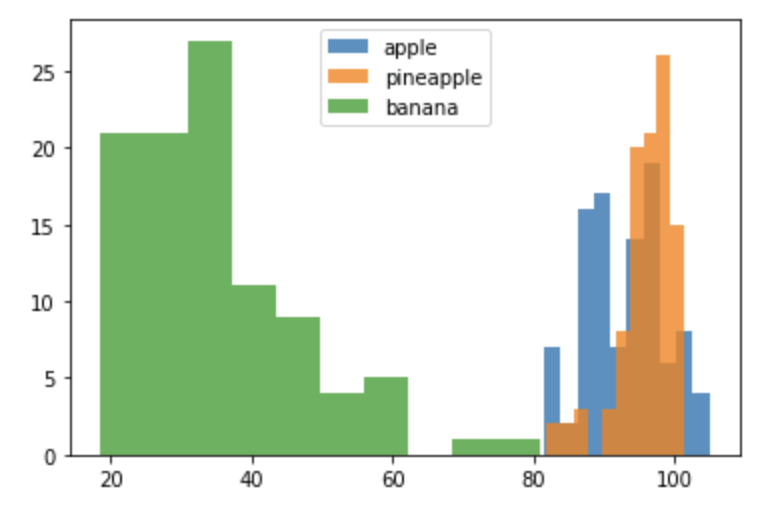
fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].bar(range(10000), np.mean(apple, axis=0))
axs[1].bar(range(10000), np.mean(pineapple, axis=0))
axs[2].bar(range(10000), np.mean(banana, axis=0))
plt.show()
apple_mean = np.mean(apple, axis=0).reshape(100, 100)
pineapple_mean = np.mean(pineapple, axis=0).reshape(100, 100)
banana_mean = np.mean(banana, axis=0).reshape(100, 100)
fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].imshow(apple_mean, cmap='gray_r')
axs[1].imshow(pineapple_mean, cmap='gray_r')
axs[2].imshow(banana_mean, cmap='gray_r')
plt.show()
평균값과 가까운 사진 고르기
abs_diff = np.abs(fruits - apple_mean)
abs_mean = np.mean(abs_diff, axis=(1,2))
print(abs_mean.shape)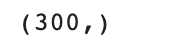
apple_index = np.argsort(abs_mean)[:100]
fig, axs = plt.subplots(10, 10, figsize=(10,10))
for i in range(10):
for j in range(10):
axs[i, j].imshow(fruits[apple_index[i*10 + j]], cmap='gray_r')
axs[i, j].axis('off')
plt.show()
| 군집(clustering) 비슷한 샘플끼리 그룹으로 모으는 작업 군집은 대표적인 비지도 학습 작업 중 하나이다. |
| 클러스터(cluster) 군집 알고리즘에서 만든 그룹 |
06-2 k-평균
k-평균 알고리즘 소개
| k-평균 군집 알고리즘 평균값을 자동으로 찾아준다. 이 평균값이 클러스터의 중심에 위치하기 때문에 클러스터 중심 또는 센트로이드라고도 부른다. |
KMeans 클래스
!wget https://bit.ly/fruits_300_data -O fruits_300.npyimport numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_2d)print(km.labels_)
print(np.unique(km.labels_, return_counts=True))
import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 샘플 개수입니다
# 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
rows = int(np.ceil(n/10))
# 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n: # n 개까지만 그립니다.
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()draw_fruits(fruits[km.labels_==0])
draw_fruits(fruits[km.labels_==1])
draw_fruits(fruits[km.labels_==2])
클러스터 중심
draw_fruits(km.cluster_centers_.reshape(-1, 100, 100), ratio=3)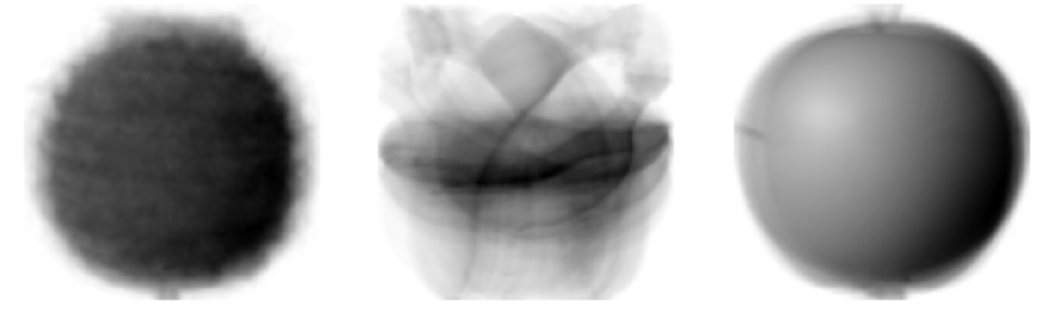
print(km.transform(fruits_2d[100:101]))
print(km.predict(fruits_2d[100:101]))
draw_fruits(fruits[100:101])
print(km.n_iter_)
최적의 k 찾기
| 이너셔(inertia) 클러스터의 샘플이 얼마나 가깝게 있는지를 나타내는 값 클러스터 중심과 클러스터에 속한 샘플 사이의 거리의 제곱 합 |
| 엘보우(elbow) 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법 |
inertia = []
for k in range(2, 7):
km = KMeans(n_clusters=k, random_state=42)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()
06-3 주성분 분석
차원과 차원 축소
| 차원 축소(dimentsionality reduction) 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도학습 모델의 성능을 향상시킬 수 있는 방법 |
주성분 분석 소개
| 주성분(principal component) 주성분 벡터는 원본 데이터에 있는 분산이 큰 방향이다. |
PCA 클래스
!wget https://bit.ly/fruits_300_data -O fruits_300.npyimport numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)print(pca.components_.shape)import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 샘플 개수입니다
# 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
rows = int(np.ceil(n/10))
# 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n: # n 개까지만 그립니다.
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()draw_fruits(pca.components_.reshape(-1, 100, 100))
print(fruits_2d.shape)
fruits_pca = pca.transform(fruits_2d)print(fruits_pca.shape)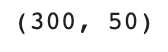
원본 데이터 재구성
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")


설명된 분산
| 설명된 분산(explained variance) 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값 |
print(np.sum(pca.explained_variance_ratio_))
plt.plot(pca.explained_variance_ratio_)
다른 알고리즘과 함께 사용하기
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()target = np.array([0] * 100 + [1] * 100 + [2] * 100)from sklearn.model_selection import cross_validate
scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
pca = PCA(n_components=0.5)
pca.fit(fruits_2d)print(pca.n_components_)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)print(np.unique(km.labels_, return_counts=True))
for label in range(0, 3):
draw_fruits(fruits[km.labels_ == label])
print("\n")


for label in range(0, 3):
data = fruits_pca[km.labels_ == label]
plt.scatter(data[:,0], data[:,1])
plt.legend(['apple', 'banana', 'pineapple'])
plt.show()
혼공머신 미션
기본 미션 - k-평균 알고리즘 작동 방식 설명하기
1. 무작위로 k개의 클러스터 중심을 정한다.
2. 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다.
3. 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경한다.
4. 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복한다.

선택 미션 - Ch.06(06-3) 확인 문제 풀고, 풀이 과정 정리하기
1. 특성이 20개인 대량의 데이터셋이 있습니다. 이 데이터셋에서 찾을 수 있는 주성분 개수는 몇 개일까요?
주성분 개수는 데이터셋에 포함된 특성의 수 중에서 작은 값에 해당합니다. 즉, 데이터셋에 포함된 특성의 수가 20개이므로, 주성분 개수는 20개 이하입니다.
2. 샘플 개수가 1,000개이고 특성 개수는 100개인 데이터셋이 있습니다. 즉 이 데이터셋의 크기는 (1000, 100)입니다. 이 데이터를 사이킷런의 PCA 클래스를 사용해 10개의 주성분을 찾아 변환했습니다. 변환된 데이터셋의 크기는 얼마일까요?
10개의 주성분을 찾아 변환한 경우, 변환된 데이터셋의 크기는 (1000, 10)입니다. 특성의 개수가 100개에서 10개로 줄어들었고, 샘플(행)의 개수인 1000개는 변화가 없습니다. PCA의 목적은 데이터의 주요 구조를 유지하면서 특성의 수를 줄이는 것이므로, 변환된 데이터셋은 원래의 데이터셋과 비슷한 구조를 가지면서, 특성의 수가 10개로 줄어든 형태입니다.
3. 2번 문제에서 설명된 분산이 가장 큰 주성분은 몇 번째인가요?
PCA는 데이터의 분산이 가장 큰 방향으로 주성분을 구하는 방법입니다. 따라서, 분산이 가장 큰 주성분은 PCA 계산 결과에서 가장 첫 번째 주성분입니다.
'ML & DL > 책 & 강의' 카테고리의 다른 글
| [밑시딥 1] CHAPTER 1 헬로 파이썬 (0) | 2023.06.05 |
|---|---|
| [혼공머신] Chapter 07 딥러닝을 시작합니다 (0) | 2023.02.19 |
| [혼공머신] Chapter 05 트리 알고리즘 (0) | 2023.02.05 |
| [혼공머신] Chapter 04 다양한 분류 알고리즘 (0) | 2023.01.22 |
| [혼공머신] Chapter 03 회귀 알고리즘과 모델 규제 (0) | 2023.01.15 |




댓글