반응형
2.1 자연어 처리란
- 자연어: 한국어와 영어 등 우리가 평소에 쓰는 말 (부드러운 언어)
- 인공어: 프로그래밍 언어, 마크업 언어 등 (딱딱한 언어)
- 자연어 처리: ‘자연어를 처리하는 분야’ = 우리의 말을 컴퓨터에게 이해시키기 위한 기술
2.1.1 단어의 의미
- 단어는 의미를 가지는 말의 최소 단위이다.
- 따라서 자연어를 컴퓨터에게 이해시키는 첫 단계는 ‘단어의 의미’를 이해시키는 것이다.
- 세 가지 기법
- 시소러스를 활용한 기법: 시소러스(유의어 사전)을 이용
- 통계 기반 기법: 통계 정보로부터 단어를 표현
- 추론 기반 기법: 구체적으로는 word2vec (3장)
2.2 시소러스
- 이렇게 모든 단어에 대한 유의어 집합을 만든 다음, 단어들의 관계를 그래프로 표현하여 단어 사이의 연결을 정의한다.
- 이 ‘단어 네트워크’를 이용하여 컴퓨터에게 단어 사이의 관계를 가르칠 수 있다.
- 예를 들면 검색 엔진에서 “car”의 검색 결과에 “automobile”의 검색 결과도 포함시켜주는 것이 있다.


2.2.1 WordNet
- WordNet
- https://wordnet.princeton.edu/
- 자연어 처리에서 가장 유명한 시소러스
- 프린스턴 대학교에서 1985년부터 구축하기 시작한 전통있는 시소러스
- WordNet을 사용해 단어 사이의 유사도도 구할 수 있다.
- 부록 B. WordNet 맛보기 참고

wordnet은 동의어 뿐 아니라 상, 하위어도 표현이 되고 있어서 아래와 같은 그래프도 만들 수 있다.

2.2.2 시소러스의 문제점
- 시대 변화에 대응하기 어렵다: 신조어 같은 경우에는 계속 갱신해야 한다
- 사람을 쓰는 비용은 크다: 현존하는 영어 단어의 수는 1,000만 개가 넘으며 이 단어 사이의 관계를 정의해야 한다. 참고로 WordNet에 등록된 단어는 20만 개 이상이라고 한다.
- 단어의 미묘한 차이를 표현할 수 없다: 시소러스에는 뜻이 비슷한 단어들이 있는데, ‘빈티지’ ‘레트로’와 같이 의미가 같은데 용법이 다른 미묘한 차이를 표현할 수 없다.
- -> 그래서 나온 방법이 ‘통계 기반 기법’ 과 ‘추론 기반 기법’!
2.3 통계 기반 기법
- 말뭉치: 자연어 처리 연구나 애플리케이션을 염두에 두고 수집된 대량의 텍스트 데이터
- 통계 기반 기법의 목표: 사람의 지식으로 가득찬 말뭉치에서 자동으로, 효율적으로 핵심을 추출하는 것
2.3.1 파이썬으로 말뭉치 전처리하기

2.3.2 단어의 분산 표현
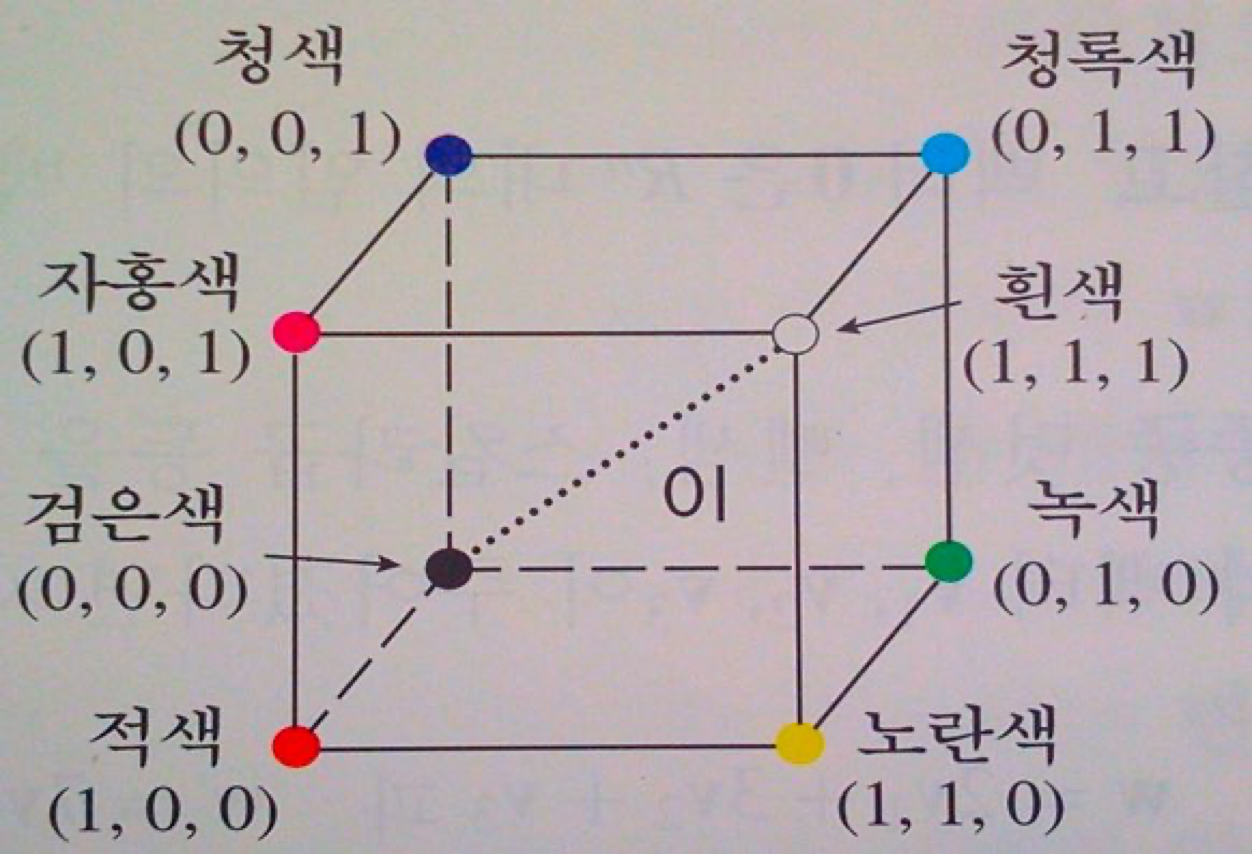
- 모든 색을 RGB 형태로 나타낼 수 있는 것 처럼, 단어도 벡터(ex. [0.21, -0.45, 0.83])로 표현할 수 있다.
- 이를 단어의 분산 표현(distributional representation)이라고 한다.

2.3.3 분포 가설
- 단어를 벡터로 표현하는 연구는 많이 이루어져 왔다.
- 그 연구들의 뿌리는 “단어의 의미는 주변 단어에 의해 형성된다”는 아이디어.
- 이를 분포 가설(distributional hypothesis)이라고 한다.
- 단어 자체에는 의미가 없고, 그 단어가 사용된 맥락이 의미를 형성한다는 것
- I drink beer. We drink wine. -> beer 와 wine이 비슷한 의미가 있구나!
- I guzzle beer. We guzzle wine -> drink랑 guzzle이 비슷한건가봐!
- 맥락은 주변에 놓인 단어를 가리킨다.
- 윈도우 크기: 주변 단어를 몇 개나 포함할 지의 크기

2.3.4 동시발생 행렬
- 분포 가설에 기초하여 단어를 벡터로 나타내는 가장 간단한 방법은 주변 단어를 ‘세어 보는 것’. 어떤 단어 주변에 어떤 단어가 몇 번이나 등장하는지를 세어서 집계하는 방법
- -> 통계 기반 기법

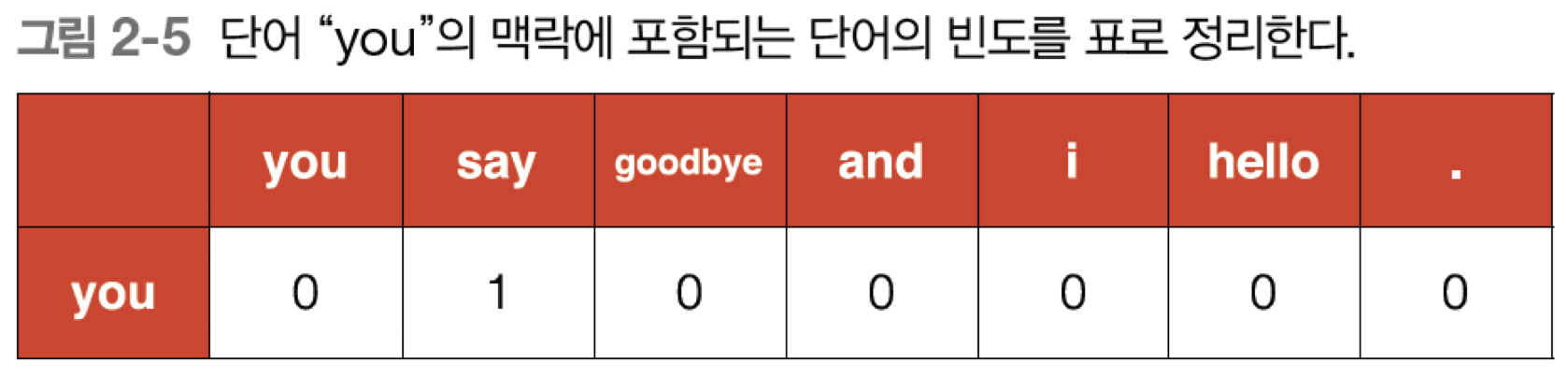
- -> 이를 바탕으로 “you”라는 단어는 [0, 1, 0, 0, 0, 0, 0] 벡터로 표현할 수 있다.


2.3.5 벡터 간 유사도
- 벡터 사이의 유사도를 측정하는 방법: 벡터의 내적, 유클리드 거리 등
- 단어 벡터 사이의 유사도 측정: 코사인 유사도(cosine similarity)

- 분자는 벡터 내적, 분모는 각 벡터의 L2 Norm -> 벡터를 정규화하고 내적했다!
- 정규화 했으므로 크기는 -1 ~ 1. 분자인 내적은 가리키는 방향이 얼마나 같은지 이므로, 완전히 같다면 1, 완전히 반대라면 -1 이 된다.

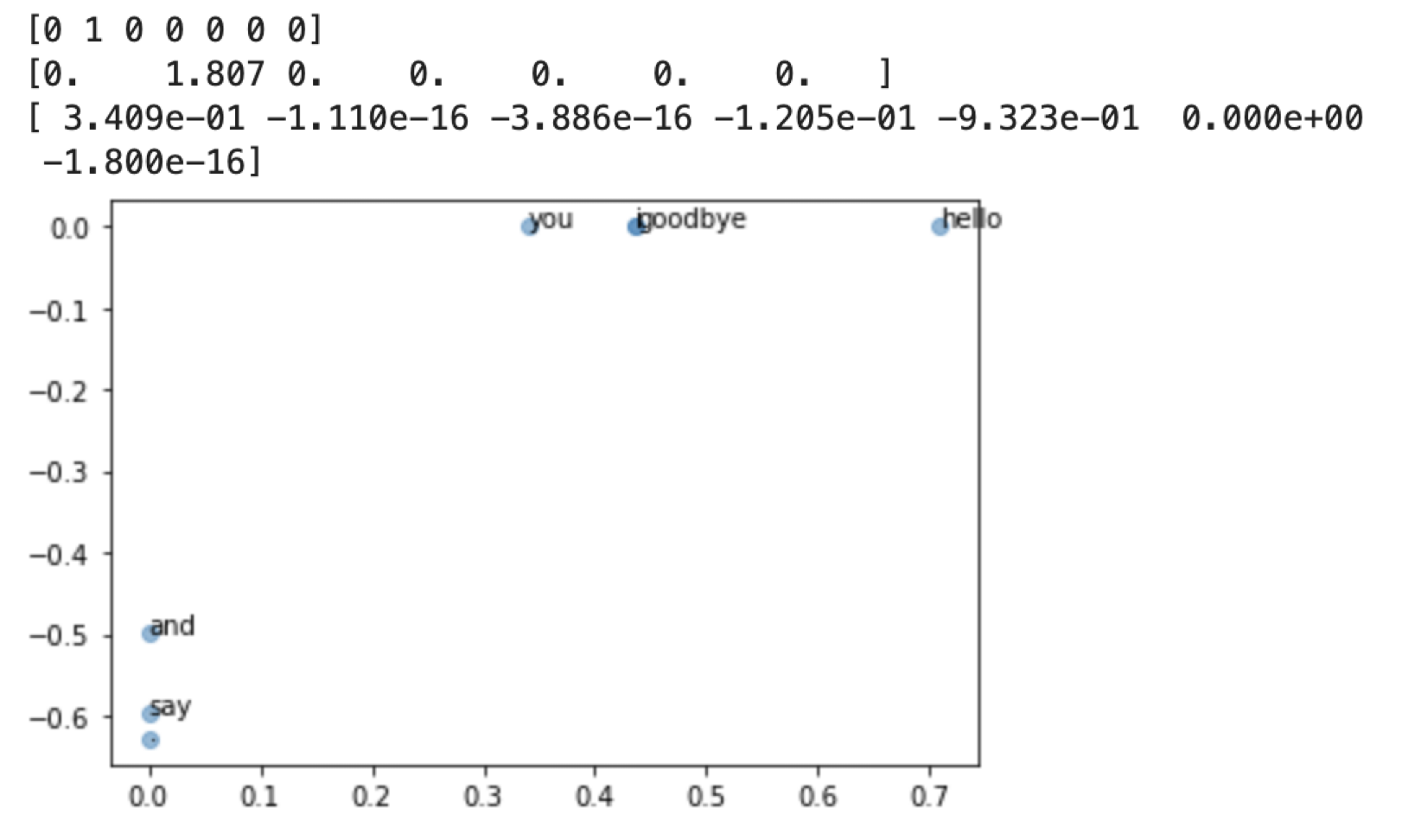
- 코사인 유사도로 단어의 유사도 구하기

- 코사인 유사도 값은 -1 ~ 1 사이이므로, 이 값은 비교적 높다. = 유사성이 크다.
2.3.6 유사 단어의 랭킹 표시


- you랑 goodbye가 유사도가 높다고? 이상해!
- 말뭉치가 너무 작기 때문!
2.4 통계 기반 기법 개선하기
2.4.1 상호정보량
- 앞서 배운 동시발생 행렬의 원소는 두 단어가 동시에 발생한 횟수를 나타낸다. 그러나 이 ‘발생 횟수’라는 게 좋은 특징일까?
- ‘The’, ‘car’의 동시발생을 생각해보면 ‘the car’라는 문구는 ‘drive car’보다 많이 나타나므로 car는 drive보다 the와 더 유사할까? 아니다!
- 이러한 문제를 해결하기 위해 점별 상호정보량(Pointwise Mutual Information(PMI))라는 척도를 사용한다.
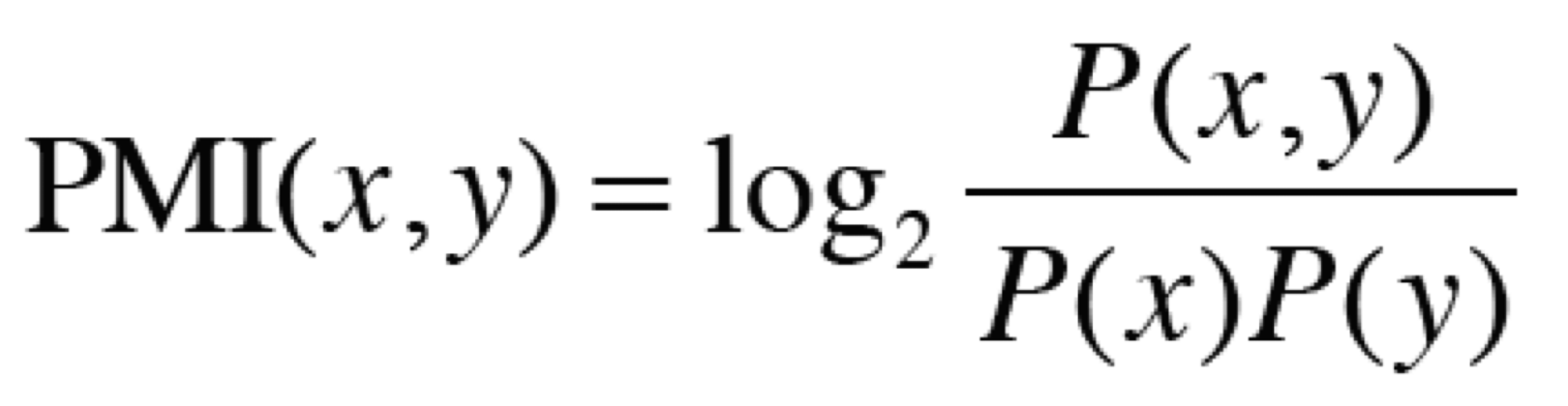
- 동시발생 행렬을 사용하여 PMI 식을 다시 써보자.
- C는 동시발생 행렬, C(x, y)는 x, y가 동시발생하는 횟수, C(x), C(y)는 각각 등장 횟수.
- N은 말뭉치에 있는 모든 단어 수

- N = 10,000
- The: 1000번 등장, car: 20번, drive: 10번 등장
- The, car 동시발생 수 10회, car, drive 동시발생 수 5회
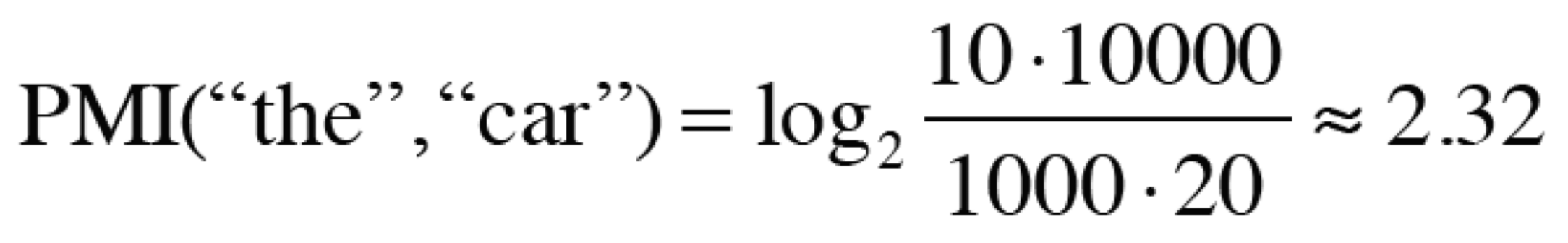

- 그러나 PMI 의 문제: 두 단어의 동시발생 횟수가 0이 된다면 log0 = - 무한대가 되어버린다.
- 이 문제를 피하기 위해 양의 상호정보량(PPMI. Positive PMI)을 사용한다.


- PPMI 행렬의 문제
- 1. 말뭉치의 어휘 수가 증가하면 단어 벡터의 차원 수도 증가한다.
- 2. 원소 대부분이 0이다. 벡터의 원소 대부분이 중요하지 않다는 뜻. 이런 벡터는 노이즈에 약하고 견고하지 않다.
- -> 이 문제들을 해결하기 위해 수행하는 방법이 벡터의 차원 감소이다.
2.4.2 차원 감소
- 차원 감소(dimensionality reduction): 문자 그대로 벡터의 차원을 줄이는 방법
- 그냥 막 줄이는 게 아니라, 중요한 정보는 최대한 유지하면서 줄여야 한다.

- 차원 감소 방법은 여러 가지이지만 책에서는 특잇값분해(Singular Value Decomposition. SVD)를 이용한다.
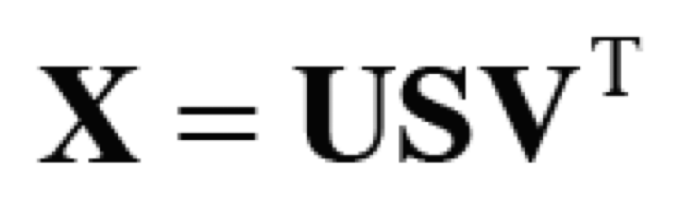
- 행렬 X를 U, S, V 세 행렬의 곱으로 분해. 여기서 U, V는 직교행렬(orthogonal matrix)이고, S는 대각행렬(diagonal matrix)이다.

- U를 ‘단어 공간’으로 생각하자.
- S의 대각성분에는 ‘특잇값 singular value’이 큰 순서로 나열되어 있다.
- 특잇값: ’해당 축’의 중요도
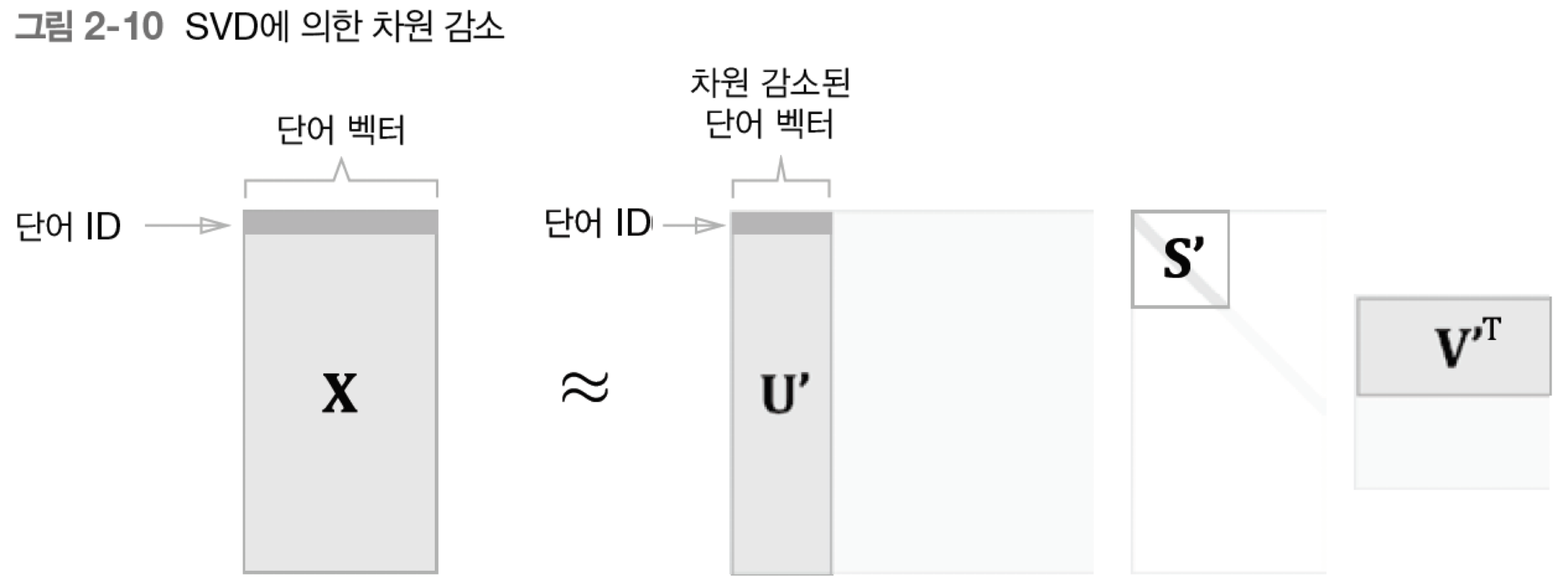
- 행렬 S에서 특잇값이 작다면 중요도가 낮으므로 버릴 수 있다.
- -> 행렬 U에서도 해당하는 열벡터를 버린다.
2.4.3 SVD에 의한 차원 감소

2.4.4 PTB 데이터셋
- 펜 트리뱅크(Penn Treebank, PTB)
- 본격적인 말뭉치
- 너무 크지도 않고 적당함
- 주어진 기법의 품질을 측정하는 벤치마크로 자주 이용
- https://paperswithcode.com/dataset/penn-treebank

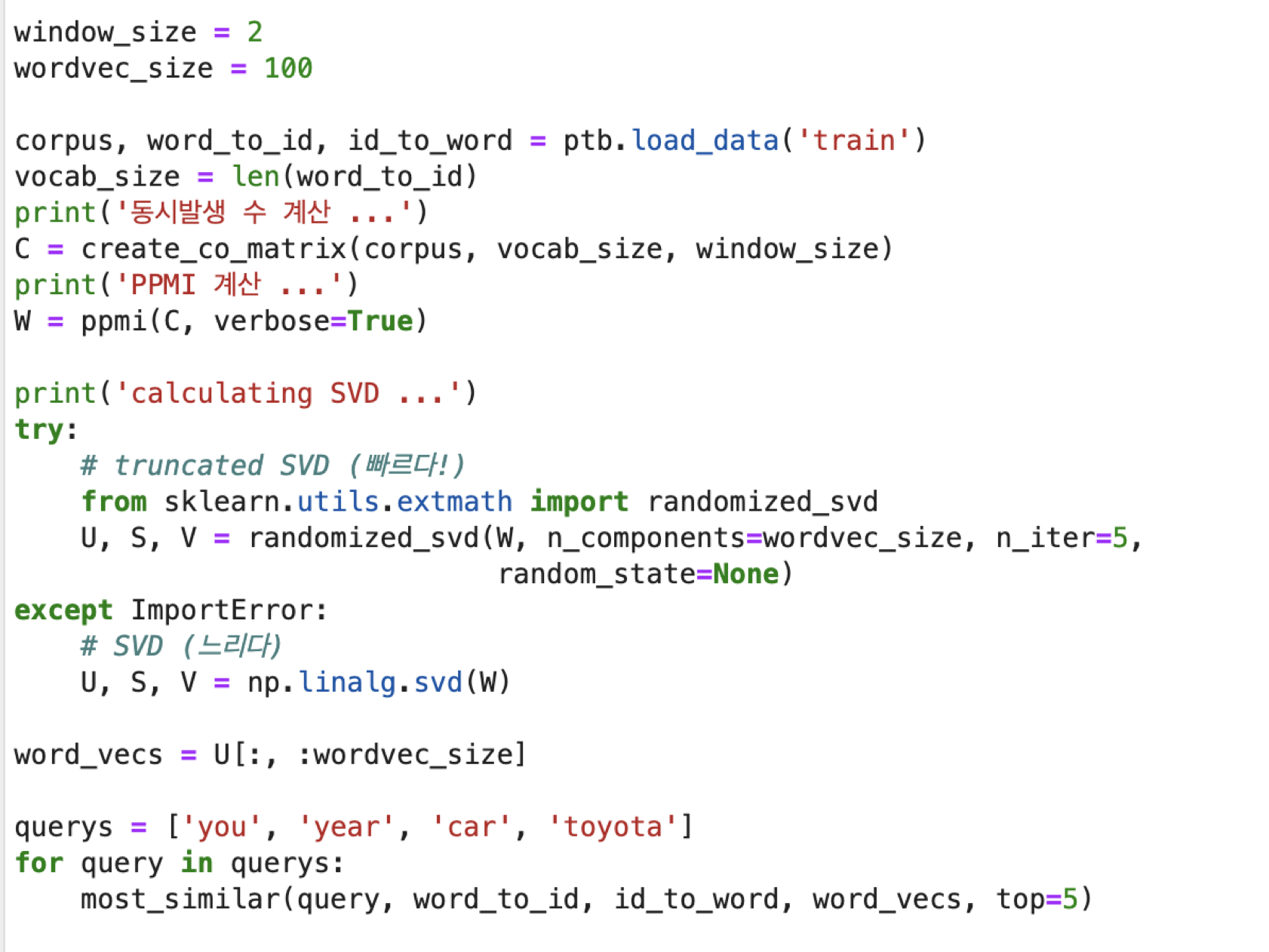

- PTB 데이터셋에 통계 기반 기법 적용
- 말뭉치를 사용해서 맥락에 속한 단어의 등장 횟수를 센 후,
- PPMI 행렬로 변환
- SVD를 이용해 차원을 감소 시킴
- -> 더 좋은 단어 벡터를 얻었다! 이것이 단어의 분산 표현. 각 단어는 고정 길이의 밀집 벡터로 표현되었다.
2.5 정리
- WordNet 등의 시소러스를 이용하면 유의어를 얻거나 단어 사이의 유사도를 측정하는 등 유용한 작업을 할 수 있다.
- 시소러스 기반 기법은 시소러스를 작성하는 데 엄청난 인적 자원이 든다거나 새로운 단어에 대응하기 어렵다는 문제가 있다.
- 현재는 말뭉치를 이용해 단어를 벡터화하는 방식이 주로 쓰인다.
- 최근의 단어 벡터화 기법들은 대부분 ‘단어의 의미는 주변 단어에 의해 형성된다’는 분포 가설에 기초한다.
- 통계 기반 기법은 말뭉치 안의 각 단어에 대해서 그 단어의 주변 단어의 빈도를 집계한다(동시발생 행렬).
- 동시발생 행렬을 PPMI 행렬로 변환하고 다시 차원을 감소시킴으로써, 거대한 ‘희소벡터’를 작은 ‘밀집벡터’로 변환할 수 있다.
- 단어의 벡터 공간에서는 의미가 가까운 단어는 그 거리도 가까울 것으로 기대된다.
반응형
'ML & DL > 책 & 강의' 카테고리의 다른 글
| [밑시딥2] CHAPTER 5 순환 신경망(RNN) (1) | 2023.07.21 |
|---|---|
| [밑시딥2] CHAPTER 3 word2vec (0) | 2023.07.12 |
| [밑시딥2] CHAPTER 1 신경망 복습 (0) | 2023.07.03 |
| [밑시딥1] CHAPTER 8 딥러닝 (0) | 2023.07.03 |
| [밑시딥1] CHAPTER 7 합성곱 신경망(CNN) (1) | 2023.06.26 |




댓글