퍼셉트론은 1957년에 고안된 알고리즘이다. 이런 화석 같은 알고리즘을 왜 배우는가? 퍼셉트론이 딥러닝의 기원이 되는 알고리즘이기 때문이다.
2.1 퍼셉트론이란?
퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력한다.

그림의 원을 뉴런 혹은 노드라고 부른다. 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다(w1, w2)
뉴런에서 보내온 신호의 총합이 임계값을 넘으면 1을 출력. 그 임계값은 세타로 나타낸다.

2.2 단순한 논리 회로
2.2.1 AND 게이트
AND 게이트 진리표

2.2.2 NAND 게이트와 OR 게이트
NAND 게이트 진리표

OR 게이트 진리표

2.3 퍼셉트론 구현하기
2.3.1 간단한 구현부터

AND 함수 구현
import numpy as np
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
2.3.2 가중치와 편향 도입
세타를 -b로 치환하여 식 수정

여기서 b는 편향(bias)라고 하고, w1, w2는 그대로 가중치(weight)

2.3.3 가중치와 편향 구현하기
AND 구현
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
가중치: 각 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수
편향: 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수
NAND 게이트 구현
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = NAND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
OR 구현
import numpy as np
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = OR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
2.4 퍼셉트론의 한계
2.4.1 도전! XOR 게이트
XOR 게이트 진리표

지금까지 본 퍼셉트론으로는 XOR게이트를 구현하지 못한다. 직선 하나로 영역을 나누는 것이 불가능하기 때문

2.4.2 선형과 비선형
퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다는 한계가 있다.
아래와 같이 곡선으로 영역을 나눌 수 있다면 XOR도 표현할 수 있을 텐데, 퍼셉트론은 그게 안된다.
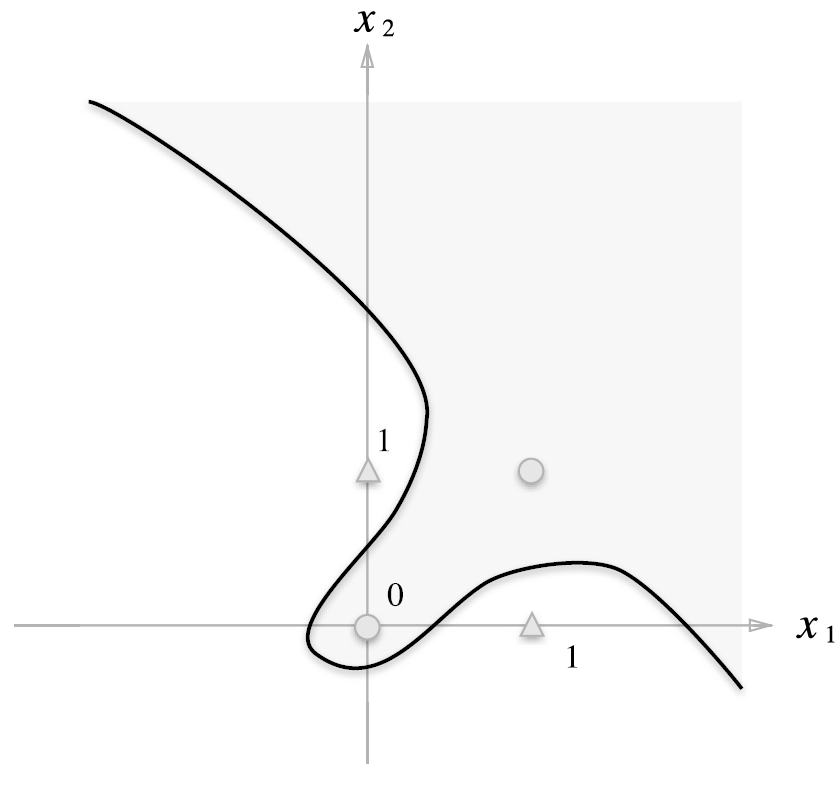
이러한 곡선의 영역을 비선형 영역, 직선의 영역을 선형 영역이라고 한다.
2.5 다층 퍼셉트론이 출동한다면
퍼셉트론으로는 XOR게이트를 표현할 수 없었지만, 층을 쌓아 다층 퍼셉트론을 만든다면 가능하다!
2.5.1 기존 게이트 조합하기
XOR 게이트를 앞서 만든 AND, NAND, OR 게이트를 조합하여 만들어보자.

위 조합이 정말 XOR를 구현하는지 진리표를 통해 확인해 보자.

2.5.2 XOR 게이트 구현하기
from and_gate import AND
from or_gate import OR
from nand_gate import NAND
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
2.6 NAND에서 컴퓨터까지
다층 퍼셉트론은 더 복잡한 회로도 만들 수 있다. 심지어 컴퓨터까지 만들 수 있다.
c.f) NAND에서 테트리스까지! ≪The Elements of Computing Systems: Building a Modern Computer from First Principles≫(The MIT Press, 2005)
2.7 정리
- 퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
- 퍼셉트론에서는 '가중치'와 '편향'을 매개변수로 설정한다.
- 퍼셉트론으로 AND, OR 게이트 등의 논리 회로를 표현할 수 있다.
- XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.
- 2층 퍼셉트론을 이용하면 XOR 게이트를 표현할 수 있다.
- 단층 퍼셉트론은 지선형 영역만 표현할 수 있고, 다층 펴셉트론은 비선형 영역도 표현할 수 있다.
- 다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.
'ML & DL > 책 & 강의' 카테고리의 다른 글
| [밑시딥 1] CHAPTER 4 신경망 학습 (2) | 2023.06.15 |
|---|---|
| [밑시딥 1] CHAPTER 3 신경망 (0) | 2023.06.13 |
| [밑시딥 1] CHAPTER 1 헬로 파이썬 (0) | 2023.06.05 |
| [혼공머신] Chapter 07 딥러닝을 시작합니다 (0) | 2023.02.19 |
| [혼공머신] Chapter 06 비지도 학습 (0) | 2023.02.12 |




댓글